Matrizes
Introdução
Conjuntos Homogêneos Multidimensionais:
Vimos até aqui vetores como conjuntos homogêneos unidimensionais. Todas as variáveis são do mesmo tipo, e acessamos usando um único índice.
int array[100];
scanf("%d", &array[0]);
No entanto, em computação, frequentemente precisamos de vetores multidimensionais.
Por exemplo: voltando aquele exemplo antigo de guardar as notas das 3 provas de cada aluno de uma turma, aprendemos que poderíamos criar 3 vetores de notas dos alunos (1 vetor para cada prova), sem a necessidade de ter 120 variáveis.
double prova1[40], prova2[40], prova3[40];
Mas e se agora existissem 100 avaliações? ou então N avaliações (indefinido) ?
double prova1[40], prova2[40], prova3[40], ... , prova98[40], prova99[40], prova100[40];
Se torna totalmente inviável criar 100 vetores para resolver este problema, sendo assim, o interessante é que cada aluno possa ser um vetor de notas. Precisamos de um vetor de vetores, mais conhecido como vetor multidimensional.

Podemos também declarar vetores com várias dimensões, tantas quanto forem necessárias.
int exemplo1[10][20][30], exemplo2[130][200][150][50];
Deve se atentar ao tamanho do vetor declarado, seu tamanho é definido pela multiplicação de suas dimensões, sendo o limite máximo aceito pelo judge 108 posições, caso contrário irá exceder o limite de memória (MLE).
int array[1000][1000][1000] // Tamanho de 10³ x 10³ x 10³ = 10^9
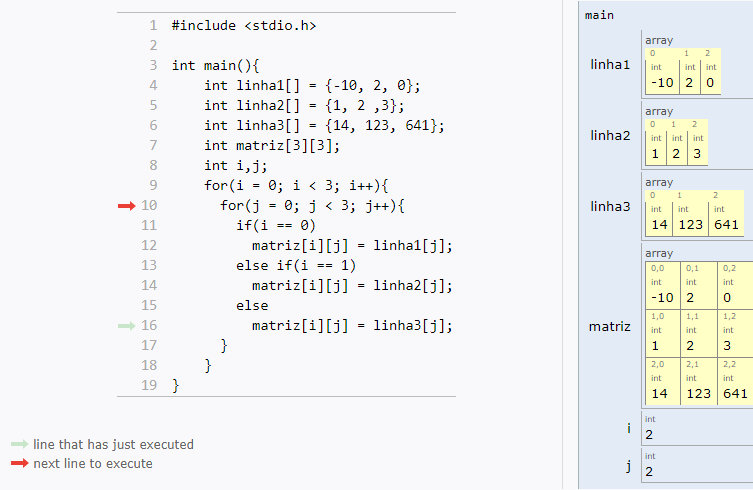
Matrizes
O que são:
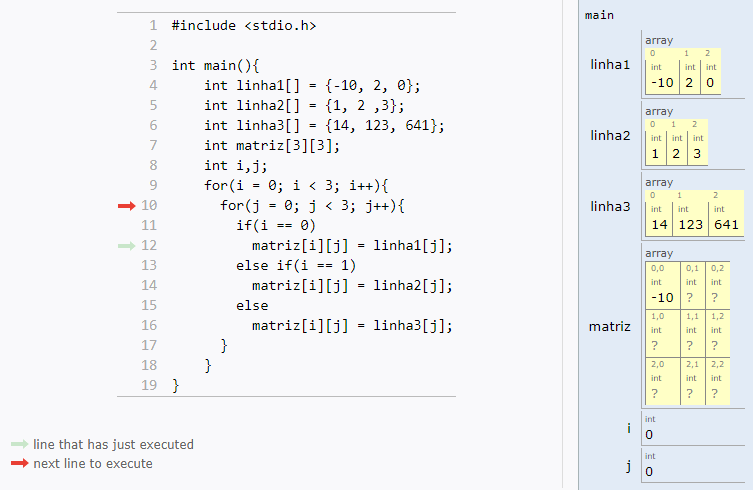
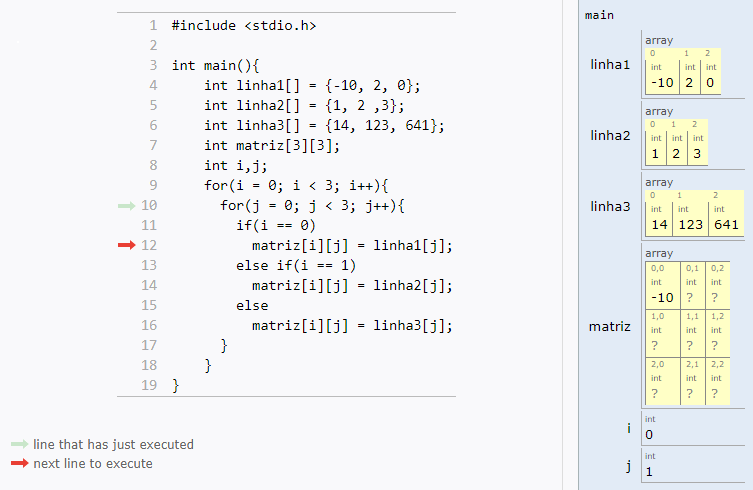
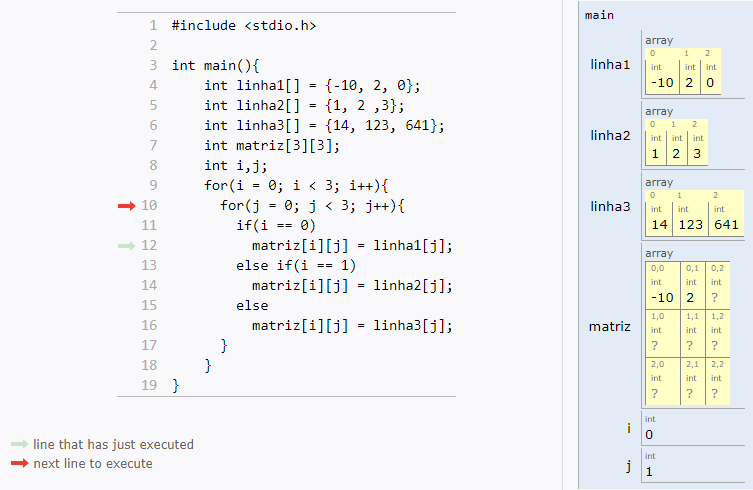
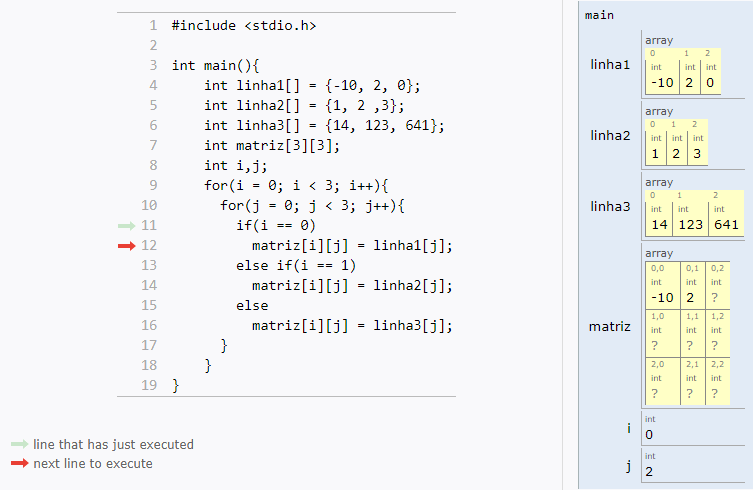
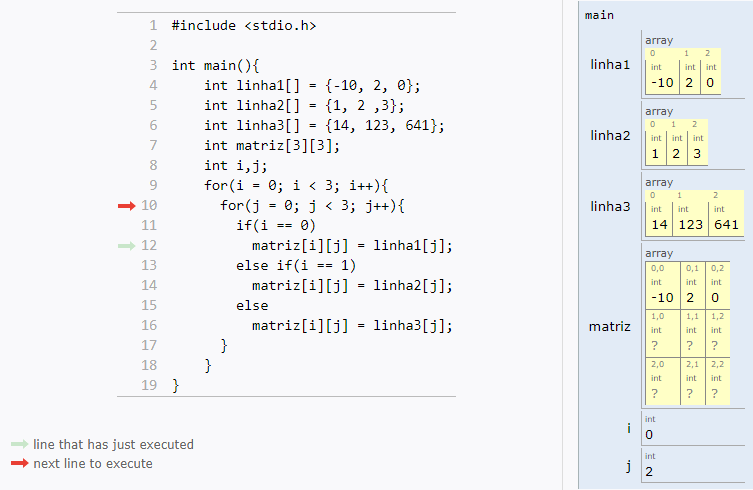
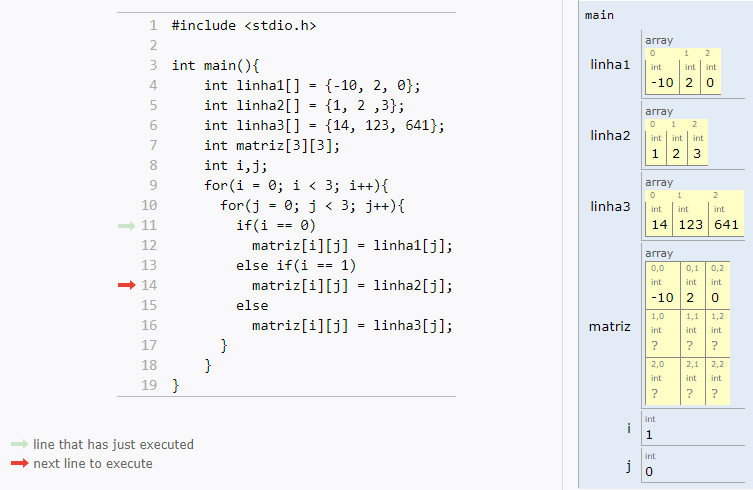
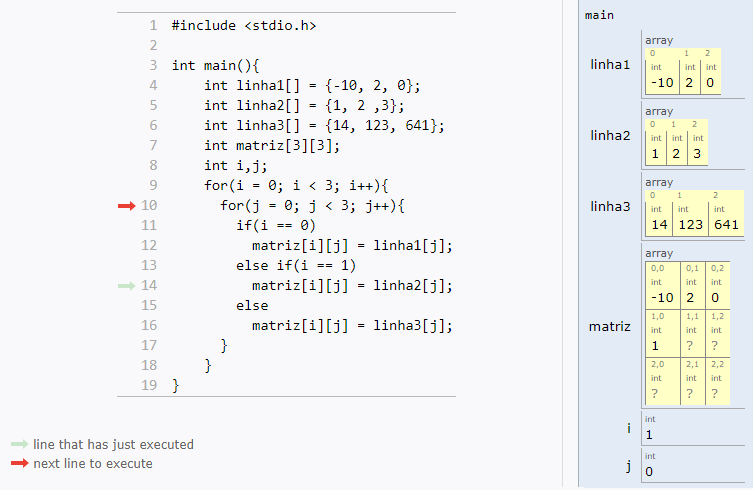
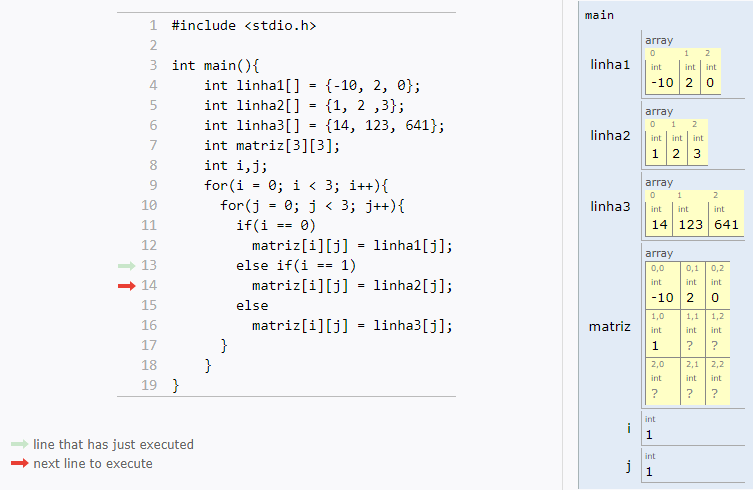
Matrizes são vetores bidimensionais, usadas com mais frequência.
Uma matriz é uma tabela com n linhas e m colunas:
Como você já deve imaginar, trabalhar com matrizes em C é muito parecido com vetores.
Os índices continuam indo de zero até tamanho-1, e você só vai adicionar uma nova dimensão (mais um par de colchetes).
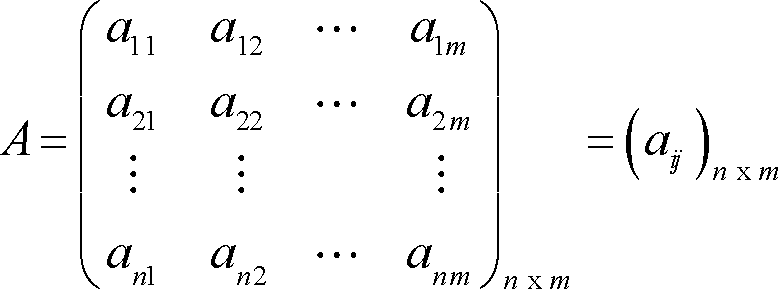
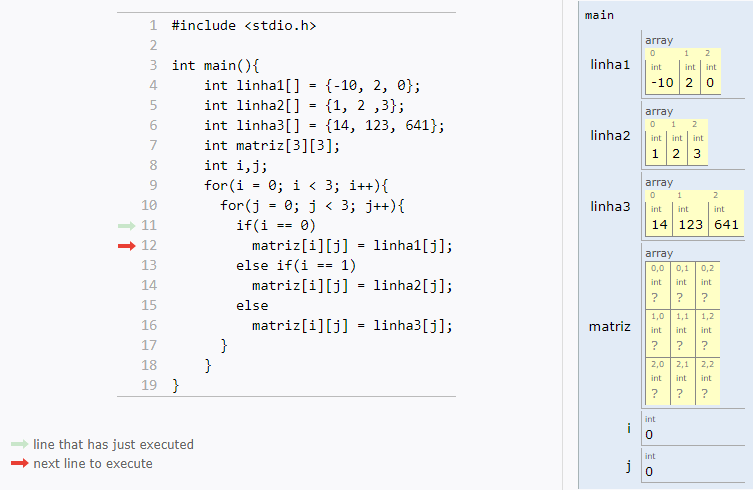
Matrizes como Parâmetros de Funções
Já sabemos como podemos passar vetores como parâmetros de funções, existem duas alternativas:
void func(int* array); // alternativa 1 - ponteiro void func(int array[]); // alternativa 2 - vetor
Para vetores de mais dimensões utilizaremos a alternativa 2, passar como vetores. Além disso, indicar o tamanho do vetor nos colchetes, para o caso unidimensional, é opcional, mas para os segundos colchetes em diante é obrigatório.
void func(int mat[][M]); // indicar M é obrigatório void func(double mat[][M][P]); // matrizes de mais dimensões funcionam igual
O motivo de termos que indicar os tamanhos das dimensões diferentes da primeira é abordado em detalhes na seção Materiais Extras. A utilização da matriz dentro da função é idêntica a outras matrizes em C.
Example
#include <stdio.h>
#include <stdlib.h> // for rand()
#define ROWS 5
#define COLUMS 5
// conta os numeros pares em uma matriz
int countEven(int m[ROWS][COLUMS]){
int r = 0, i, j;
for(i = 0; i < ROWS; i++){
for(j = 0; j < COLUMS; j++){
if(m[i][j]%2 == 0)
r++;
}
}
return r;
}
// mostra uma matriz na tela
void printMat(int m[][COLUMS]){ // note que ROWS eh opcional. COLUMS nao.
int i, j;
for(i = 0; i < ROWS; i++){
for(j = 0; j < COLUMS; j++)
printf("%d ", m[i][j]);
printf("\n");
}
}
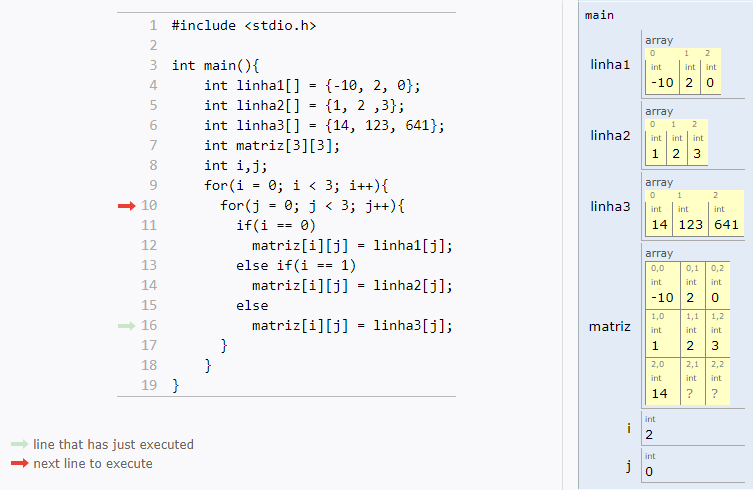
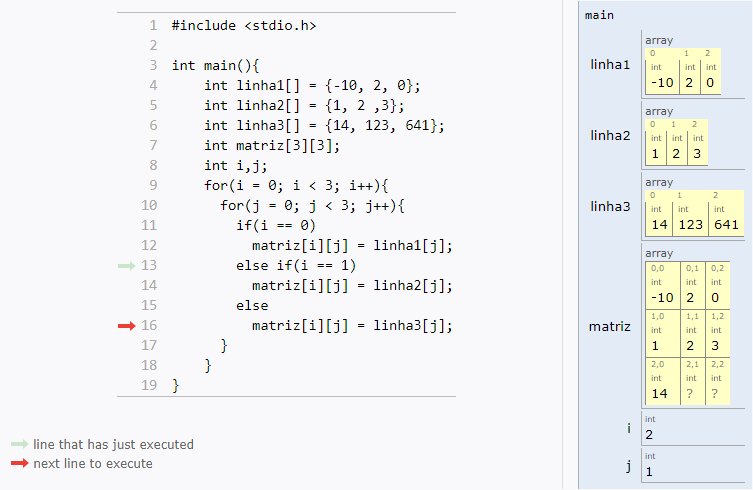
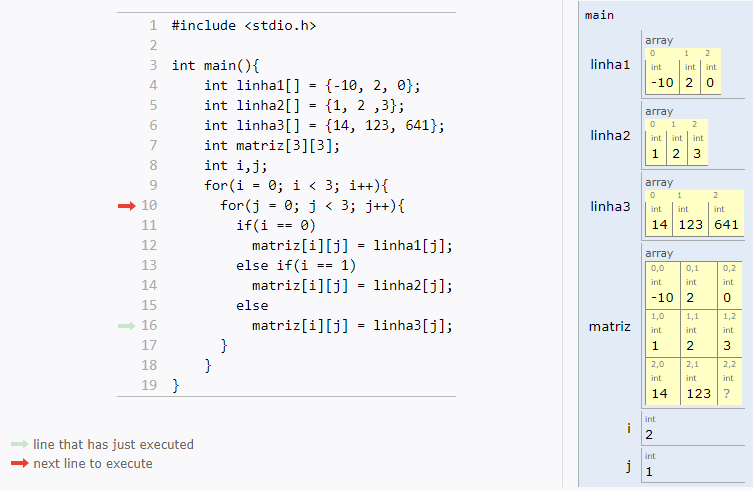
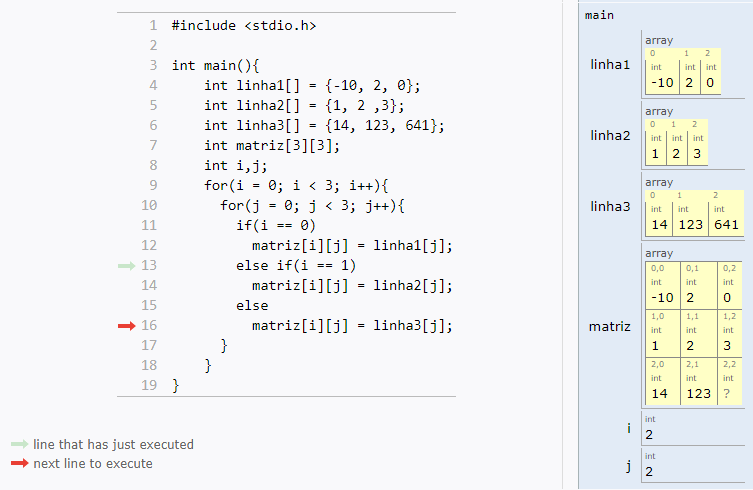
int main(){
int matriz[ROWS][COLUMS];
int i,j;
for(i = 0; i < ROWS; i++)
for(j = 0; j < COLUMS; j++)
matriz[i][j] = rand() % 100;
int even = countEven(matriz);
printf("Existem %d numeros pares na matriz\n", even);
printMat(matriz);
}
Download Code
Code Execution
Para mais exemplos visite este site. Ele inclui também a opção 1, passar matrizes como ponteiros, mas ela é mais complicada (veja seção Materiais Extras para saber o porquê)
Exercícios Recomendados
Materiais Extras
Vetores multidimensionais na memória
Na sessão Matrizes como Parâmetros de Funções vimos que só podemos passar matrizes como vetores para usá-las em funções, e é obrigatório informar o tamanho das dimensões, exceto a primeira. Isso acontece pela forma como os vetores são salvos na memória, e como o computador calcula os endereços dos elementos do vetor.
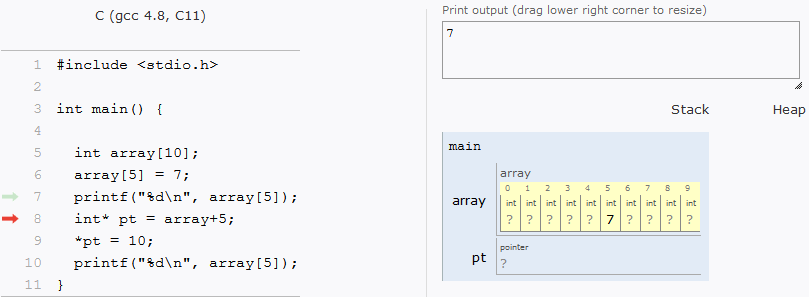
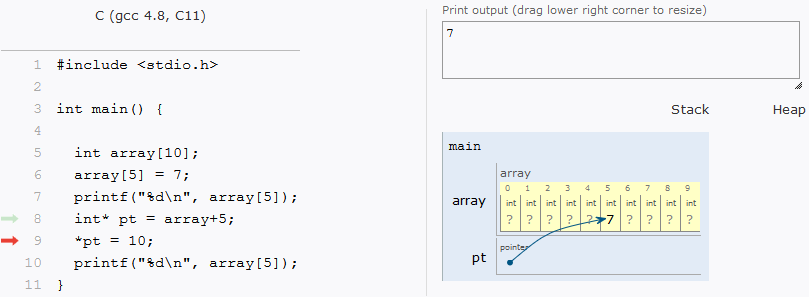
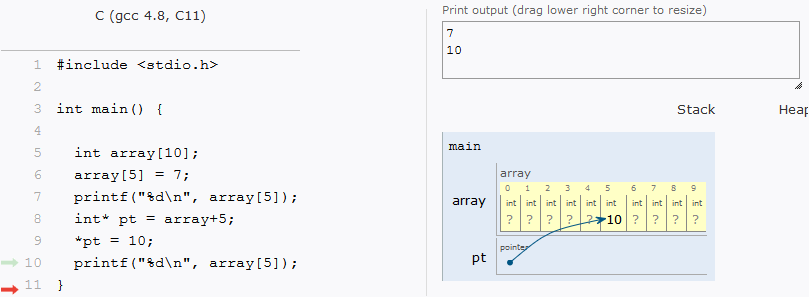
Os elementos de um vetor estão salvos em posições contíguas na memória. Isto vale para array de qualquer dimensão. Assim, a seguinte matriz:
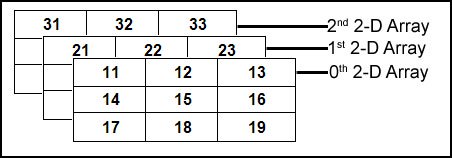
Na verdade, na memória do computador, fica organizada em uma única dimensão:

Como os elementos estão em posições contíguas, seus endereços também são contíguos. Logo, para saber o endereço de um elemento em qualquer array unidimensionais, o computador só precisa fazer o cálculo addr = array + idx*sizeof(type) onde addr é o endereço procurado, array é o primeiro endereço do vetor, idx é a posição desejada e type é o tipo do vetor. Por exemplo
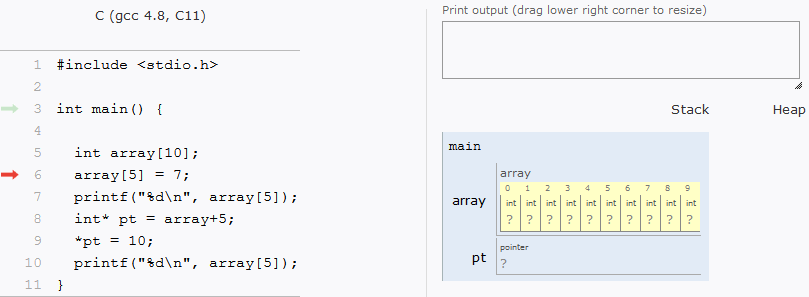
Isso é perfeitamente possível de ser feito porque o computador sabe quantos bytes pular para chegar em qualquer elemento, já que todos ocupam um espaço definido pelo tipo do vetor. No entanto, se queremos, por exemplo, pular uma linha inteira de uma matriz, como saber qual o tamanho da linha? Não é possível, a menos que saibamos de antemão. Como o tamanho de uma linha é igual ao número de colunas * tamanho de cada elemento, conclui-se que precisamos informar o tamanho das colunas, para que o computador possa fazer o cálculo dos endereços. Assim, se não especificamos este tamanho (por exemplo, se passarmos uma matriz para uma função como ponteiro) temos que fazer o cálculo nós mesmos.
Veja vários exemplos de como passar matrizes como parâmetros de funções neste site.