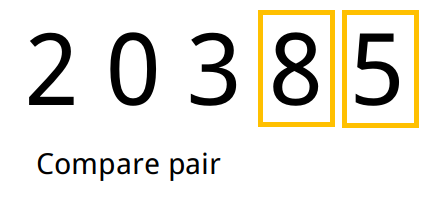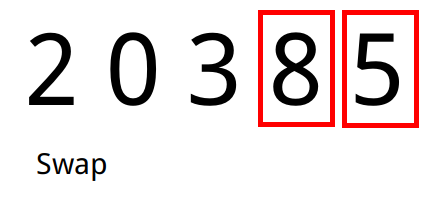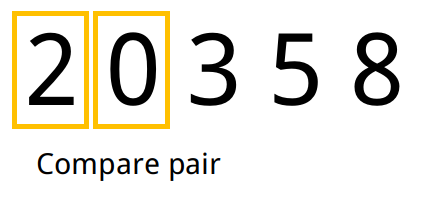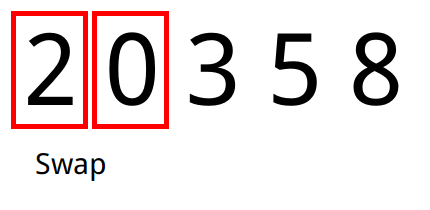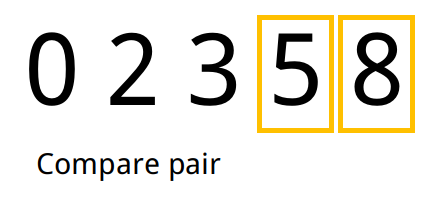Busca & Ordenação
Introdução
Busca
Busca é um método bastante utilizado em programação, pois frequentemente necessitamos de informações que podem ser adquiridas através dela.
Pode-se realizar busca em diversos lugares como: vetores (verificação da existência de um valor dentro dele), intervalos numéricos (qual o melhor ponto dentro de um intervalo que satisfaz o problema), strings (se um letra está contida em uma string) e etc.
Trataremos neste capítulo da pesquisa sequencial e da pesquisa binária.
Ordenação
A ordenação consiste em dispor elementos em uma certa sequência, seguindo algum critério. Por exemplo, a ordenação lexicográfica (alfabética) para dados literais, ou crescente e decrescente para dados numéricos.
Existem muitos algoritmos de ordenação conhecidos: InsertionSort, ShellSort, BubbleSort, HeapSort, MergeSort , QuickSort, dentro Outros.
Aqui veremos o BubbleSort. Outros algoritmos de ordenação serão vistos na matéria de Estruturas de Dados.
Busca Linear
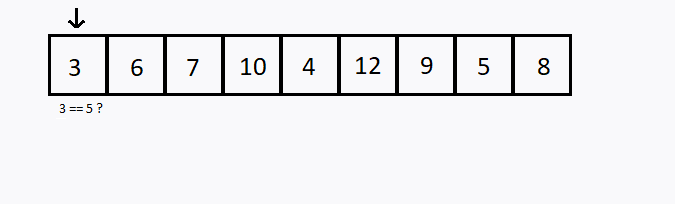
Vamos supor que temos 4 portas fechadas, e atrás de cada porta contém 1 número, qual estratégia poderíamos tomar para encontrar o número 3?
O método trivial seria abrir qualquer porta aleatoriamente enquanto não encontrar o número 3.
Obviamente este método não é nem de perto o mais eficiente.
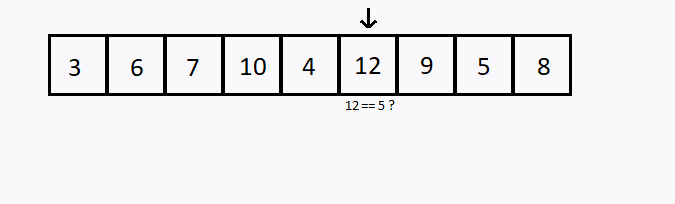
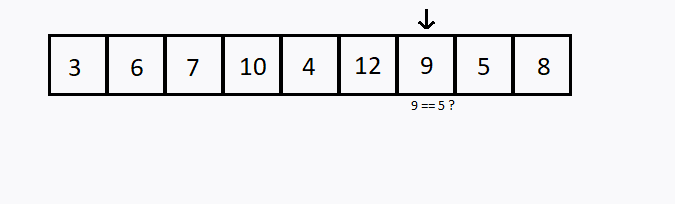
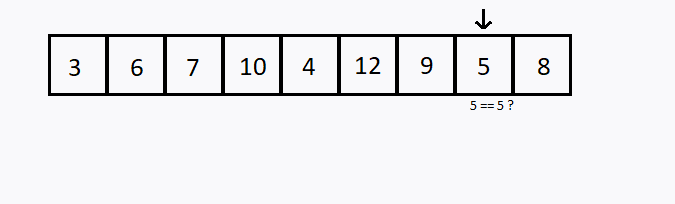
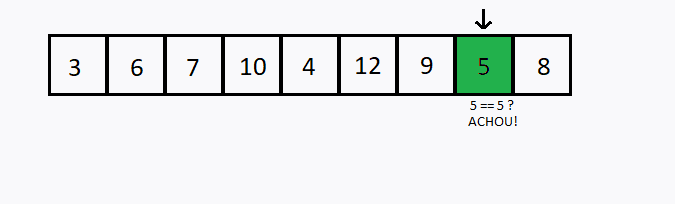
Outra estratégia seria começando na primeira porta e ir abrindo as próximas na sequência. Este método se chama Busca Linear.
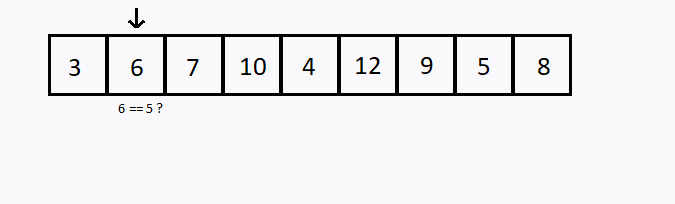
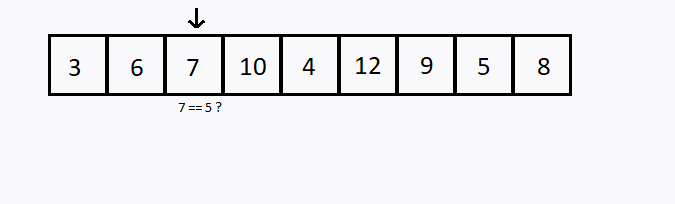
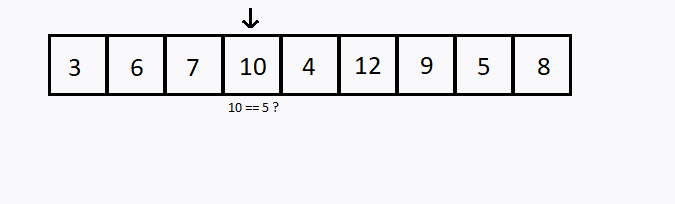
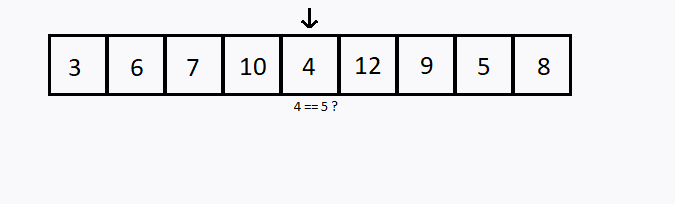
Verificamos sequencialmente (ou seja, um após o outro) cada elemento. Se encontramos o valor desejado, então a pesquisa foi bem sucedida.
Caso todos os elementos do conjunto sejam verificados e o elemento desejado não esteja entre eles, dizemos que a pesquisa foi mal sucedida.
int i, valor, achou;
int conjunto[] = {3,6,7,10,4,12,9,5,8};
valor = 5;
i = 0;
achou = 0;
while ((i < 10) && (!achou)) {
if (conjunto[i] == valor)
achou = 1;
else
i++;
}
if (achou)
printf("%d encontrado na posicao %d.\n", valor, i + 1);
else
printf("%d nao encontrado.\n", valor);
Download Code
Code Execution
Busca binária
A pesquisa binária utiliza a técnica de “dividir e conquistar”.
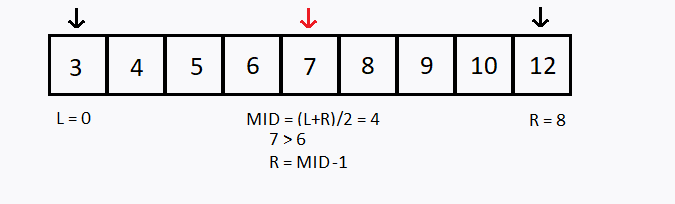
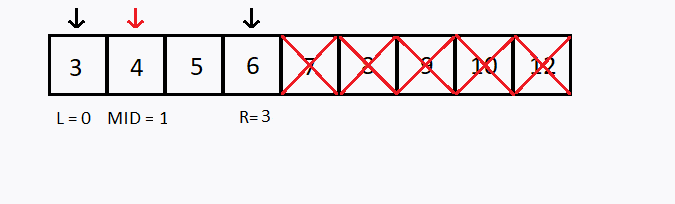
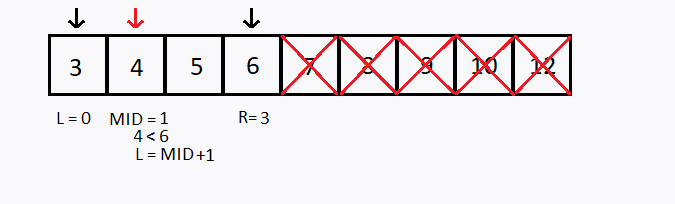
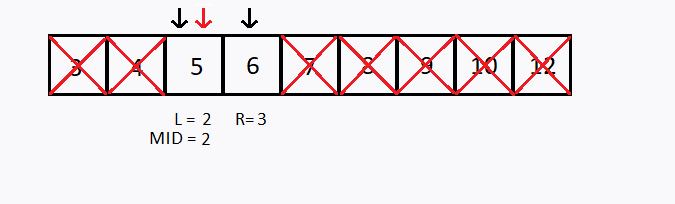
Primeiro, testamos se o elemento procurado é menor que o elemento do meio do vetor. Se for o caso, então passamos a buscar apenas na primeira metade do vetor.
Se não, testamos se o elemento procurado é maior que o elemento do meio do vetor. Se for o caso, então passamos a buscar apenas na segunda metade do vetor.
Caso contrário o valor procurado é igual ao elemento que está no meio do vetor.
- Esse procedimento é repetido até que o elemento seja encontrado ou não haja mais elementos a testar.
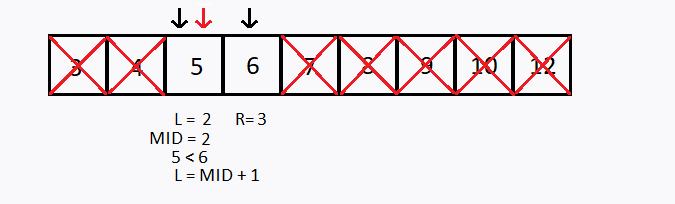
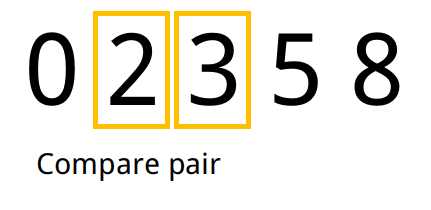
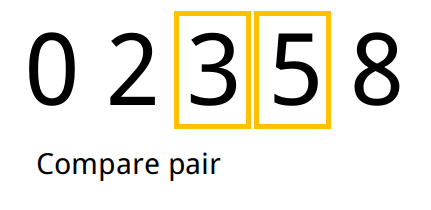
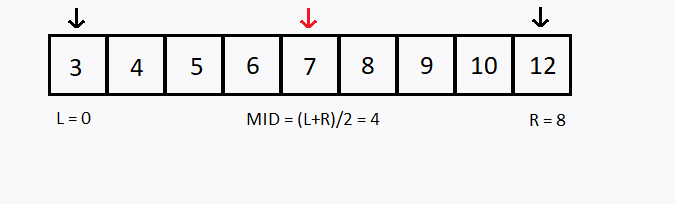
Suponha que desejamos buscar o número 6 no mesmo vetor anterior, porém agora foi informado que o vetor está ordenado em ordem crescente, como aplicar a busca binária ?
Observação 1: O vetor precisa estar ordenado para conseguir realizar a busca binária.
Observação 2: Note que, a cada teste, descartamos uma das metades do (sub)vetor pesquisado.
int inicio, fim, meio, valor, achou;
int conjunto[] = {3,4,5,6,7,8,9,10,12};
valor = 6;
inicio = 0;
fim = 8;
achou = 0;
while ((inicio <= fim) && (!achou)) {
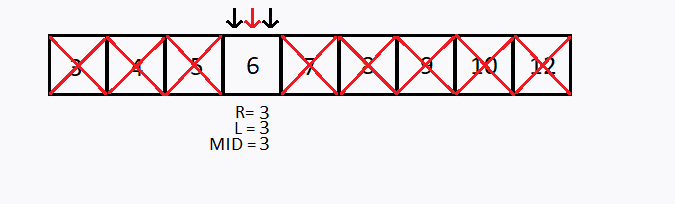
meio = (inicio + fim) / 2;
if (valor < conjunto[meio])
fim = meio - 1;
else if (valor > conjunto[meio])
inicio = meio + 1;
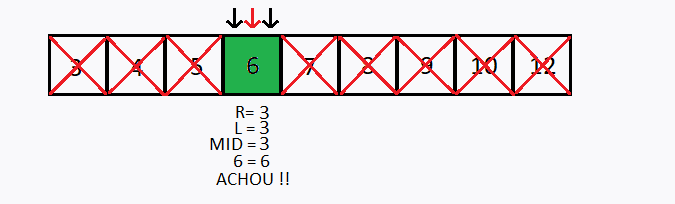
else
achou = 1;
}
if (achou)
printf("%d encontrado na posicao %d.\n", valor, meio + 1);
else
printf("%d nao encontrado.\n", valor);
Download Code
Code Execution
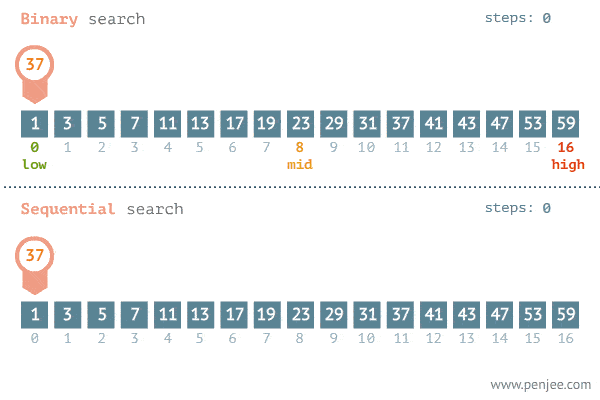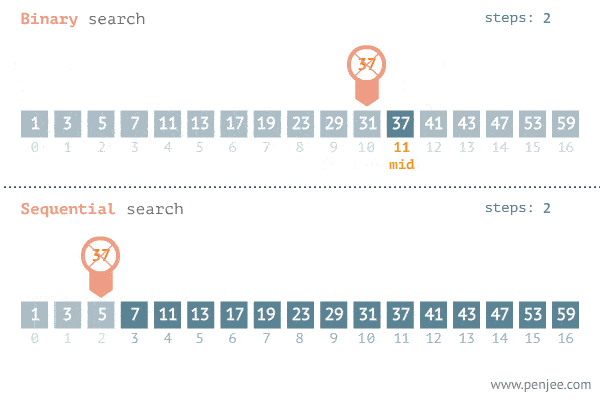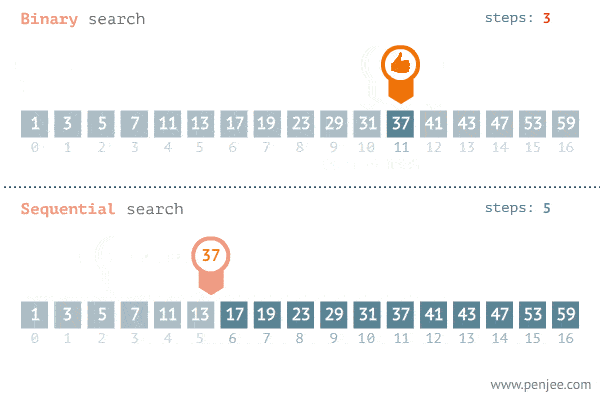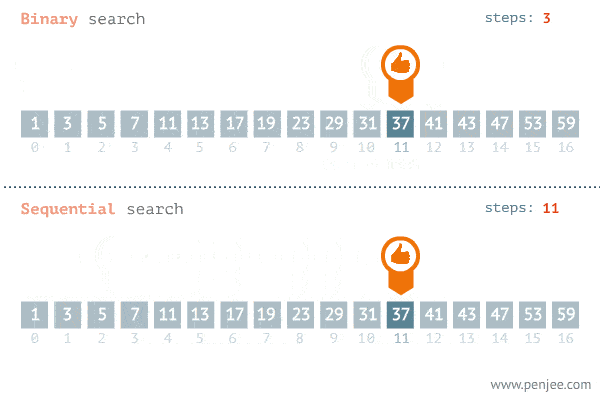
Resumindo, a eficiência da busca binária é muito superior a uma busca linear (no pior caso), pois a cada iteração metade do sub-vetor é descartada. Sua complexidade é de O(log(n)) enquanto a complexidade da busca linear é O(n) (Assunto sobre complexidade será tratado futuramente).
Segue um exemplo da comparação entre as duas buscas.
Ordenação
BubbleSort
- Ordenar uma coleção significa dispor seus elementos seguindo um critério determinado. Esta operação é bastante comum em computação, e por isso existem vários algoritmos para fazê-la. A principal diferença entre os algoritmos é sua eficiência.
- Como contato inicial vamos analisar o algoritmo BubbleSort. Ele é um algoritmo simples, apesar de não muito eficiente.
- A ideia do BubbleSort é organizar os elementos do conjunto colocando um elemento por vez no seu lugar certo. Isso reduz o tamanho do vetor a ser organizado em 1 para cada elemento que é colocado em sua posição correta.
Exemplo
Vamos analisar um exemplo de funcionamento do algoritmo antes de mostrá-lo. Suponha um vetor de inteiros com n elementos que queremos ordenar em ordem crescente.
- Tomamos o primeiro elemento e analisamos o seu sucessor no array. Caso o sucessor seja menor que o antecessor, trocamos os dois de lugar.
- Repetimos o passo 1 para todos os pares até o final do array. Ao final desse processo o elemento de maior valor ficará na última posição do array.
- Repetimos a operação n vezes, uma para cada elemento. Ao final do processo o vetor estará ordenado.
void bubbleSort(int v[], int n){
int i, j;
// passo 3
for(j = 0; j < n; j++){
// passo 2
for(i = 0; i < n-1; i++){
// passo 1
if(v[i] > v[i+1]){
int aux = v[i];
v[i] = v[i+1];
v[i+1] = aux;
}
}
}
}
int main(){
int v[] = {-10, 2, 0, 4, 6, 2, -5, 20, 7, 9};
int n = 10, i;
printf("Vetor original com %d elementos\n", n);
for(i = 0; i < n; i++)
printf("%d ", v[i]);
printf("\n");
// ordenar o vetor
bubbleSort(v, n);
printf("Vetor ordenado com %d elementos\n", n);
for(i = 0; i < n; i++)
printf("%d ", v[i]);
printf("\n");
}
Download Code
Code Execution
Pergunta: Se quisessemos organizar o vetor em ordem decrescente, o que precisaria ser mudado?
Análise Inicial do BubbleSort
Note que o vetor, ao final da execução do algoritmo, está ordenado em ordem crescente, como era o objetivo. Este algoritmo vai funcionar para qualquer vetor de inteiros. No entanto, como cientistas da computação sempre devemos estar preocupados em criar programas funcionais e eficientes. Vamos analisar este algoritmo acima:
- O algoritmo precisa percorrer o vetor inteiro várias vezes em sua execução (exatamente n² vezes).
- O número de operações a serem executadas é sempre o mesmo, indepentente de como os valores estão no vetor original, isto é, o tempo de "ordenar" um vetor já ordenado e de ordenar um vetor completamente não-ordenado, neste algoritmo, é o mesmo.
- É possível que o vetor fique ordenado antes do final da execução do algoritmo, mas ele não pára quando o vetor está ordenado, levando sempre o mesmo tempo de execução.
Com estas observações, podemos melhorar nosso algoritmo. A ideia básica continua sendo a mesma, mas a eficiência aumenta, pois melhoramos a performace dele para alguns casos mais comuns, adicionando as seguintes mudanças.
- Adicionamos uma flag "ok" para indicar se uma passada pelo vetor não produziu nenhuma mudança. Isto é, se percorremos o vetor inteiro e nenhuma mudança foi necessária, podemos parar.
- Sabemos que a cada execução do passo 2 um elemento vai para a sua posição final. Podemos tirar vantagem desse fato fazendo com que menos pares sejam comparados por iteração do loop mais interno.
void betterBubbleSort(int v[], int n){
int i, j, ok = 0;
// passo 3
for(j = 0; j < n && ok == 0; j++){
// passo 2
ok = 1;
for(i = 0; i < n-j-1; i++){
// passo 1
if(v[i] > v[i+1]){
ok = 0;
int aux = v[i];
v[i] = v[i+1];
v[i+1] = aux;
}
}
}
}
int main(){
int v[] = {-10, 2, 0, 4, 6, 2, -5, 20, 7, 9};
int n = 10, i;
printf("Vetor original com %d elementos\n", n);
for(i = 0; i < n; i++)
printf("%d ", v[i]);
printf("\n");
// ordenar o vetor
betterBubbleSort(v, n);
printf("Vetor ordenado com %d elementos\n", n);
for(i = 0; i < n; i++)
printf("%d ", v[i]);
printf("\n");
}
Download Code
Code Execution
A mudança pode parecer pequena, mas aumenta bastante a eficiência do algoritmo. Por exemplo, repare que o primeiro BubbleSort, no link de execução
possui 283 passos, enquanto o segundo só possui 190, uma melhora de quase 33%.
Uma análise mais detalhada do BubbleSort está na seção Análise do BubbleSort.
Exercícios Recomendados
| Frequência de Números | Saltos Ornamentais | Troca de Cartas |
| Frase Completa | Pares e Ímpares | A Biblioteca do Senhor Severino |
| Assigning Teams | Onde está o Mármore? | Exame Geral |
Questões desafio (Nivel: Médio / Difícil)
Materiais Extras
Análise de Algoritmos Básica
A análise de algoritmos estuda a correção e o desempenho de algoritmos.
Em outras palavras, a análise de algoritmos procura respostas para perguntas do seguinte tipo:
"Este algoritmo resolve o meu problema?
Quanto tempo o algoritmo consome para processar uma 'entrada' de tamanho n?".
A análise feita é uma estimativa de tempo (e espaço) utilizado por um determinado algoritmo independente do hardware utilizado. Esta estimativa consistem em analisar o número de operações do algoritmo para diversos casos possíveis,
em geral o melhor caso, o caso médio e o pior caso.
Definimos uma operação como uma linha de código executada, e contamos quantas vezes cada linha é executada.
No algoritmo da busca linear, por exemplo, se existir um vetor com os números: 1, 46, 4, -1, 20, caso o número buscado seja o número 1, o programa irá executar apenas uma verificação, porém este é o melhor caso para a situação e não é assim que se avalia a complexidade de um algoritmo. Sendo assim, o método correto consiste em analizar no pior caso, ou seja, quando o número não pertence ao conjunto ou ele está na última posição do vetor, necessitando de 6 operações (n operações para um vetor de tamanho n) e assim sua complexidade é linear O(n), pois para um vetor de tamanho n será necessáario n operações para completar o algoritmo.
Notação assintótica
Com a análise das operações, chegamos a uma função que descreve o crescimento do tempo de execução do algoritmo. Em geral, esta função pode ser bastante complicada, e não é tão prática de se trabalhar, por isso usamos a notação assintótica. Nesta notação, consideramos apenas o termo de maior ordem. No caso da busca linear, seria o n.
A notação assintótica que veremos é a Big-O. Ele representa um limite assintótico superior, isto quer dizer que o algoritmo pode ter uma execução melhor do que a notação indica, mas no pior caso ela será a analisada. Como em geral estamos interessados na execução do algoritmo no pior caso, a notação Big-O é muito interessante. Assim, dizemos que o algoritmo de busca linear tem ordem de complexidade O(n).
Algoritmos com limite assintótico melhor são mais eficientes, e preferíveis a outros com limites maiores.
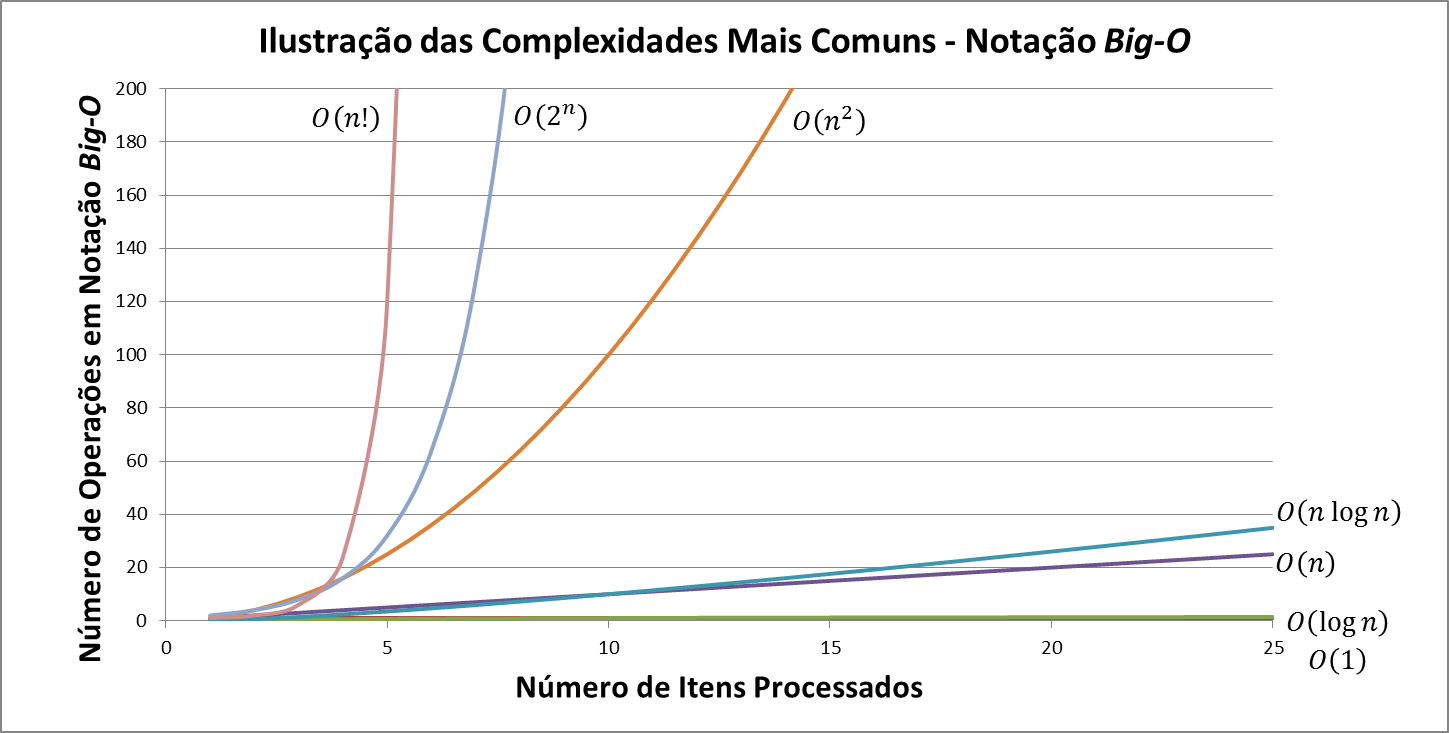
Análise do BubbleSort
Primeiramente vamos recaptular os passos necessários para a execução do algoritmo.
- Tomamos o primeiro elemento e analisamos o seu sucessor no array. Caso o sucessor seja menor que o antecessor, trocamos os dois de lugar.
- Repetimos o passo 1 para todos os pares até o final do array. Ao final desse processo o elemento de maior valor ficará na última posição do array.
- Repetimos a operação n vezes, uma para cada elemento. Ao final do processo o vetor estará ordenado.
Pegando só a função do BubbleSort, e considerando cada linha como uma operação, podemos ter uma estimativa da complexidade.
void bubbleSort(int v[], int n){
int i, j; // executado 1 vez
// passo 3 - executado n vezes
for(j = 0; j < n; j++){
// passo 2 - executado n vezes
for(i = 0; i < n-1; i++){
// passo 1
if(v[i] > v[i+1]){ // executado toda vez
int aux = v[i];
v[i] = v[i+1];
v[i+1] = aux;
}
}
}
}
- A primeira linha é executada somente 1 vez.
- O laço do passo 3 é executado n vezes.
- O laço do passo 2 é executado n vezes para cada execução do passo 3, portanto n² vezes.
- A condição if do passo 1 é executada sempre, portanto n² vezes.
Portanto a estimativa seria da ordem de 1+ 2n² + α, onde α é a quantidade de vezes que as operações internas ao if do passo 1 são executadas.
Removendo as constantes e variáveis de menor ordem temos que a complexidade do BubbleSort, assintóticamente, é O(n²). Conforme vimos na Análise Inicial
este algoritmo terá o mesmo tempo para qualquer caso. As melhorias apresentadas naquela seção aceleram o algoritmo para alguns casos. O algoritmo melhorado é O(1) no melhor caso,
mas continua O(n²) no pior caso. Uma análise mais completa do algoritmo pode ser vista. aqui.
Algoritmos de ordenação com complexidade O(n²), por exemplo, BubbleSort, Insertion Sort, Selection Sort, etc não são usados em aplicações mais complexas, pois demoram demais para vetores grandes. Por exemplo, para vetores com 10 elementos o tempo seria 10² = 100 operações. Para vetores com 100 elementos, temos 100² = 10000 operações. Para vetores com 1000 elementos, 1000² = 1000000 operações. Um computador consegue executar, em geral, 108 operações em 1 segundo. Assim, este algoritmo demora muito para vetores com muito mais de 1000 elementos.