Já sabemos como usar funções. Mas existe uma classe particular de funções que ainda não exploramos: as funções recursivas. Essas funções tem a particularidade de chamar elas mesmas durante sua execução, e são muito úteis para resolver problemas recursivos.

Os problemas recursivos são aqueles que podem ser definidos utilizando instâncias menores deles mesmos. Pos exemplo, a função fatorial é recursiva, podendo ser definida como:

Note na linha superior que a definição de n! utiliza a função fatorial em uma instância menor, i.e. (n-1)!. Isso caracteriza uma função fatorial. A segunda linha da definição define a condição de parada da função. Toda função recursiva possui uma condição de parada.

Prev GIF Next

Resumidamente temos:

• Problemas recursivos são definidos a partir de instâncias menores deles mesmos.
• Podemos utilizar funções recursivas para resolver esses problemas. Elas chamam elas mesmas em sua execução.
• Toda função recursiva precisa de um caso base, isto é, uma condição de parada.

A função de fatorial é muito simples de ser implementada, como mostrado abaixo. Note que precisamos retornar o valor calculado recursivamente para que ele chegue na chamada anterior. Se não retornarmos o valor ele será perdido. Isso é por conta da maneira que a pilha de execução funciona. Veremos isso com mais detalhes adiante.

long long factorial(int n){
    if(n == 1)  // caso base
        return 1;
    // caso recursivo
    return n * factorial(n-1);
}
                                

Veja Execução Download Code

Vamos entender então como funciona a recursividade no computador. Para isso precisamos entender melhor a pilha de execução. Os conceitos básicos são os seguintes:

• Toda vez que fazemos uma chamada de função dentro do programa, o SO reserva memória para as variáveis e parâmetros desta função.
• A função no topo da pilha é função sendo executada no momento.
• Quando uma função termina de ser executada ela é removida da pilha.
• Quando ocorre uma nova chamada de função, a função chamada é colocada imediatamente no topo da pilha e começa a ser executada.

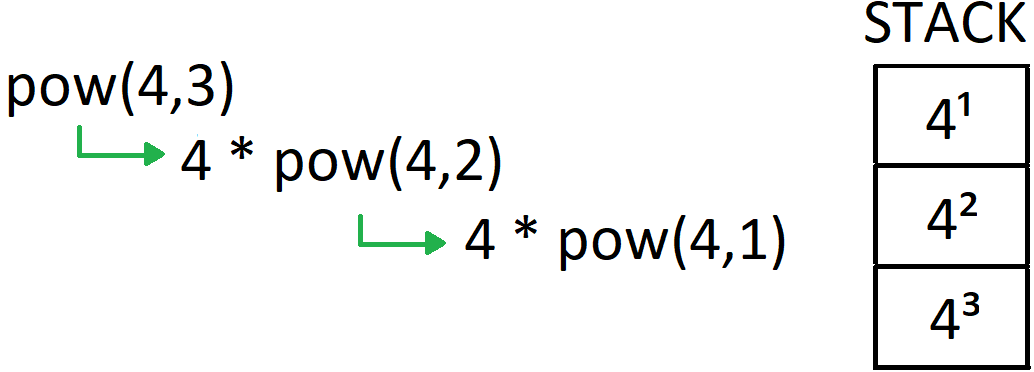
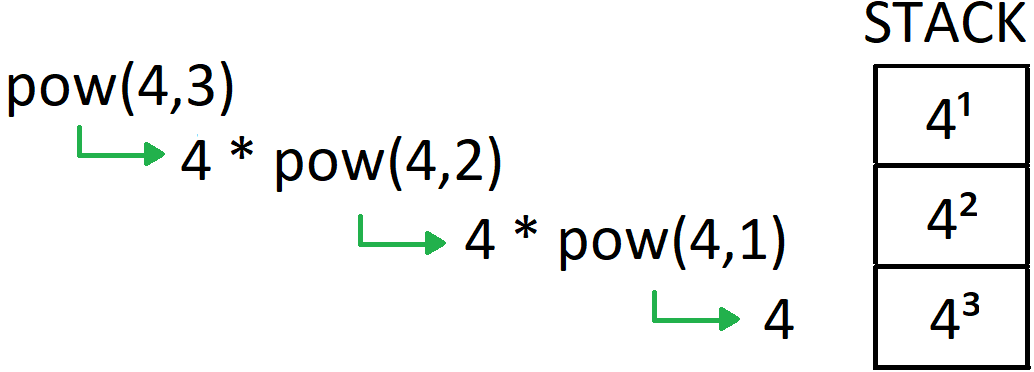
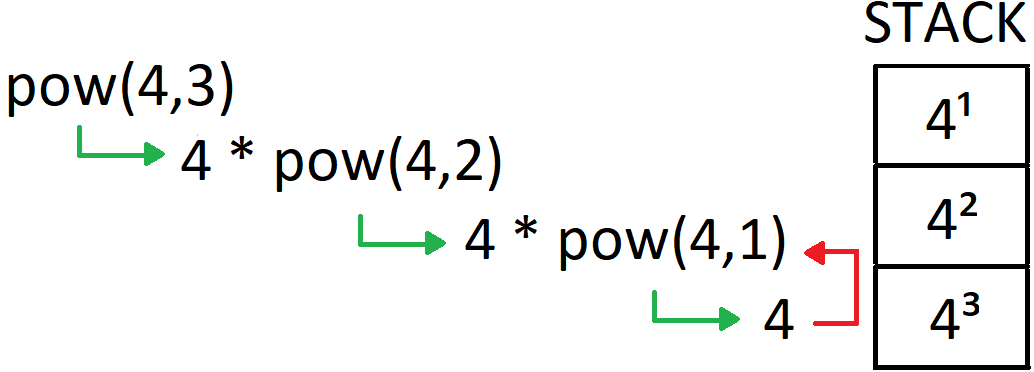
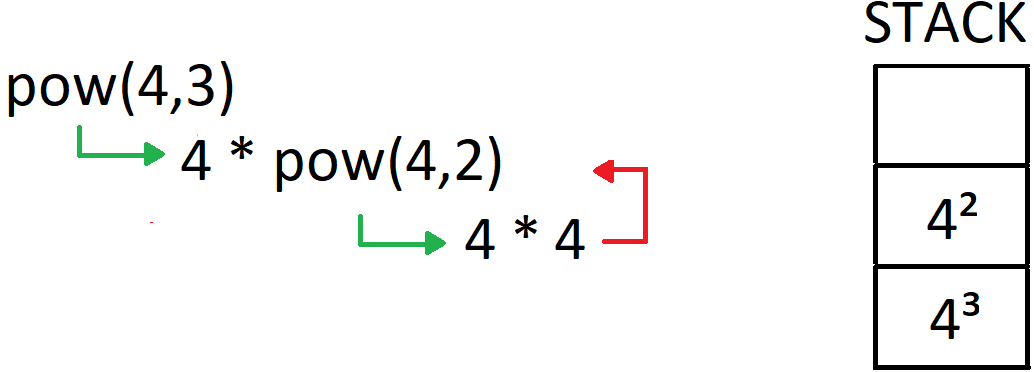
Vejamos um esquema.

Prev Next

Note que:

• Uma chamada recursiva nada mais é que uma simples chamada de função. Tudo que acontece é que várias instâncias da mesma função ficam empilhadas.
• Cada instância da função na pilha tem suas próprias variáveis locais, por isso o que acontece em uma instância de uma função recursiva não influencia o que acontece em outras instâncias.

Nada no computador é ilimitado, principalmente a memória. Pelo exemplo de funcionamento da pilha de execução você deve ter percebido que chamar funções ocupa memória. Como uma função recursiva faz várias chamadas de função temos que tomar alguns cuidados:

• Se um algoritmo recursivo faz muitas chamadas, ele pode causar um estouro de pilha (stack overflow), ou seja, ficar sem memória suficiente para continuar a execução do programa.
• Para evitar o estouro da pilha, as chamadas reecursivas precisam parar. Daí a importancia da condição de parada da função.
• Apesar de funções recursivas serem mais elegantes e mais fáceis de implementar, elas costumam ser menos eficientes que suas correspondentes iterativas, por causa do overhead de empilhar e desempilhar chamadas de funções.

Não é tão simples decidir quando usar uma solução recursiva para um problema, mas você vai perceber que alguns problemas são muito mais fáceis e intuitivos de serem resolvidos recursivamente. É nesses casos que a recursão vale a pena.

A título de curiosidade, existe um paradigma de programação, a chamada programação funcional que faz extenso uso de recursividade nas definições de estruturas de dados e funções.

int pow_recursivo(int x, int n){
    if(n == 1)
        return x;

    return x * pow_recursivo(x,n-1);
}

void add(char nome[], char c){
    int n = strlen(nome);
    nome[n] = c;
    nome[n+1] = '\0';
}

void inverter_string(char nome[], char aux[], int n){

    if(n == -1)
        return;

    add(aux,nome[n]);

    inverso(nome,aux,n-1);
}

int binary_search(int v[], int x, int L, int R){

    if(L > R)
        return -1;

    int mid = (L+R)/2;

    if(v[mid] == x)
        return mid;
    else if(v[mid] > x)
        return binary_search(v,x,L,mid-1);
    else
        return binary_search(v,x,mid+1,R);
}